#include "utilities/kdl-config.h"#include "utilities/utility.h"#include "utilities/hash_combine.h"#include <functional>#include "frames.inl"
Include dependency graph for frames.hpp:
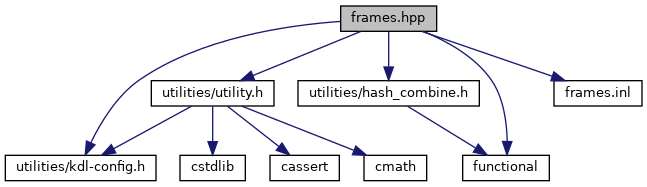
This graph shows which files directly or indirectly include this file:

Go to the source code of this file.
Classes | |
| class | KDL::Frame |
| represents a frame transformation in 3D space (rotation + translation) More... | |
| class | KDL::Frame2 |
| struct | std::hash< KDL::Frame > |
| struct | std::hash< KDL::Frame2 > |
| struct | std::hash< KDL::Rotation > |
| struct | std::hash< KDL::Rotation2 > |
| struct | std::hash< KDL::Twist > |
| struct | std::hash< KDL::Vector > |
| struct | std::hash< KDL::Vector2 > |
| struct | std::hash< KDL::Wrench > |
| class | KDL::Rotation |
| represents rotations in 3 dimensional space. More... | |
| class | KDL::Rotation2 |
| class | KDL::Twist |
| represents both translational and rotational velocities. More... | |
| class | KDL::Vector |
| A concrete implementation of a 3 dimensional vector class. More... | |
| class | KDL::Vector2 |
| 2D version of Vector More... | |
| class | KDL::Wrench |
| represents both translational and rotational acceleration. More... | |
Namespaces | |
| KDL | |
Functions | |
| IMETHOD Frame | KDL::addDelta (const Frame &F_w_a, const Twist &da_w, double dt=1) |
| IMETHOD Rotation | KDL::addDelta (const Rotation &R_w_a, const Vector &da_w, double dt=1) |
| IMETHOD Twist | KDL::addDelta (const Twist &a, const Twist &da, double dt=1) |
| adds the twist da to the twist a. see also the corresponding diff() routine. More... | |
| IMETHOD Vector | KDL::addDelta (const Vector &p_w_a, const Vector &p_w_da, double dt=1) |
| adds vector da to vector a. see also the corresponding diff() routine. More... | |
| IMETHOD Wrench | KDL::addDelta (const Wrench &a, const Wrench &da, double dt=1) |
| adds the wrench da to the wrench w. see also the corresponding diff() routine. see also the corresponding diff() routine. More... | |
| IMETHOD Twist | KDL::diff (const Frame &F_a_b1, const Frame &F_a_b2, double dt=1) |
| IMETHOD Vector | KDL::diff (const Rotation &R_a_b1, const Rotation &R_a_b2, double dt=1) |
| IMETHOD Twist | KDL::diff (const Twist &a, const Twist &b, double dt=1) |
| IMETHOD Vector | KDL::diff (const Vector &p_w_a, const Vector &p_w_b, double dt=1) |
| IMETHOD Wrench | KDL::diff (const Wrench &W_a_p1, const Wrench &W_a_p2, double dt=1) |
| bool | KDL::Equal (const Frame &a, const Frame &b, double eps=epsilon) |
| bool | KDL::Equal (const Frame2 &a, const Frame2 &b, double eps=epsilon) |
| bool | KDL::Equal (const Rotation &a, const Rotation &b, double eps) |
| bool | KDL::Equal (const Rotation2 &a, const Rotation2 &b, double eps=epsilon) |
| bool | KDL::Equal (const Twist &a, const Twist &b, double eps=epsilon) |
| bool | KDL::Equal (const Vector &a, const Vector &b, double eps=epsilon) |
| bool | KDL::Equal (const Vector2 &a, const Vector2 &b, double eps=epsilon) |
| bool | KDL::Equal (const Wrench &a, const Wrench &b, double eps=epsilon) |
| bool | KDL::operator== (const Rotation &a, const Rotation &b) |
Detailed Description
- Warning
- Efficienty can be improved by writing p2 = A*(B*(C*p1))) instead of p2=A*B*C*p1
- PROPOSED NAMING CONVENTION FOR FRAME-like OBJECTS
* A naming convention of objects of the type defined in this file : * (1) Frame : F... * Rotation : R ... * (2) Twist : T ... * Wrench : W ... * Vector : V ... * This prefix is followed by : * for category (1) : * F_A_B : w.r.t. frame A, frame B expressed * ( each column of F_A_B corresponds to an axis of B, * expressed w.r.t. frame A ) * in mathematical convention : * A * F_A_B == F * B * * for category (2) : * V_B : a vector expressed w.r.t. frame B * * This can also be prepended by a name : * e.g. : temporaryV_B * * With this convention one can write : * * F_A_B = F_B_A.Inverse(); * F_A_C = F_A_B * F_B_C; * V_B = F_B_C * V_C; // both translation and rotation * V_B = R_B_C * V_C; // only rotation *
- CONVENTIONS FOR WHEN USED WITH ROBOTS :
* world : represents the frame ([1 0 0,0 1 0,0 0 1],[0 0 0]') * mp : represents mounting plate of a robot * (i.e. everything before MP is constructed by robot manufacturer * everything after MP is tool ) * tf : represents task frame of a robot * (i.e. frame in which motion and force control is expressed) * sf : represents sensor frame of a robot * (i.e. frame at which the forces measured by the force sensor * are expressed ) * * Frame F_world_mp=...; * Frame F_mp_sf(..) * Frame F_mp_tf(,.) * * Wrench are measured in sensor frame SF, so one could write : * Wrench_tf = F_mp_tf.Inverse()* ( F_mp_sf * Wrench_sf ); *
- CONVENTIONS REGARDING UNITS :
- Any consistent series of units can be used, e.g. N,mm,Nmm,..mm/sec
- Twist and Wrench transformations
- 3 different types of transformations do exist for the twists and wrenches.
* 1) Frame * Twist or Frame * Wrench : * this transforms both the velocity/force reference point * and the basis to which the twist/wrench are expressed. * 2) Rotation * Twist or Rotation * Wrench : * this transforms the basis to which the twist/wrench are * expressed, but leaves the reference point intact. * 3) Twist.RefPoint(v_base_AB) or Wrench.RefPoint(v_base_AB) * this transforms only the reference point. v is expressed * in the same base as the twist/wrench and points from the * old reference point to the new reference point. *
- Spatial cross products
- Let m be a 6D motion vector (Twist) and f be a 6D force vector (Wrench) attached to a rigid body moving with a certain velocity v (Twist). Then
* 1) m_dot = v cross m or Twist=Twist*Twist * 2) f_dot = v cross f or Wrench=Twist*Wrench *
- Complexity
- Sometimes the amount of work is given in the documentation e.g. 6M+3A means 6 multiplications and 3 additions.
Definition in file frames.hpp.
 1.8.17
1.8.17